A thermodynamic analysis of solar sails

I wrote a simple paper to demonstrate that Carnot’s theorem is consistent with solar sails during my undergraduate studies at the Nanjing Institute of Meteorology in 2003-2004. It was originally published in Chinese in the physics education journal College Physics: 大学物理 (College Physics), 2005, 24(6): 62-62. The result probably will not have any practical use, but I still think it is an intriguiing exercise for college student. With the assistance of ChatGPT, I have translated the main section into English and am sharing it here.

Figure 1

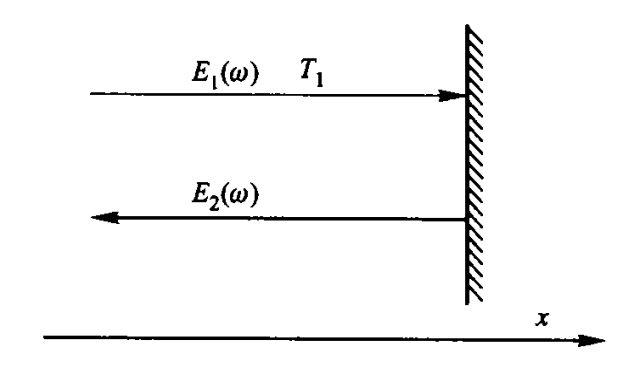
To simplify the problem, consider an idealized scenario. As shown in Figure 1, the normal vector of an ideal flat reflective mirror points in the negative x-axis direction. The energy spectral distribution of blackbody radiation from a plane wave traveling in the positive x-axis direction with temperature \(T\) can be approximated (ignoring constant coefficients) as:

\[E_1(\omega) \propto \frac{\omega^3}{e^{\hbar\omega / k T_1} - 1}\]

After reflection by the flat mirror, the energy spectral distribution becomes \(E_2(\omega)\). Below, we will demonstrate that \(E_2(\omega)\) is also the energy spectral distribution of blackbody radiation and determine the temperature of the reflected radiation.

Figure 2

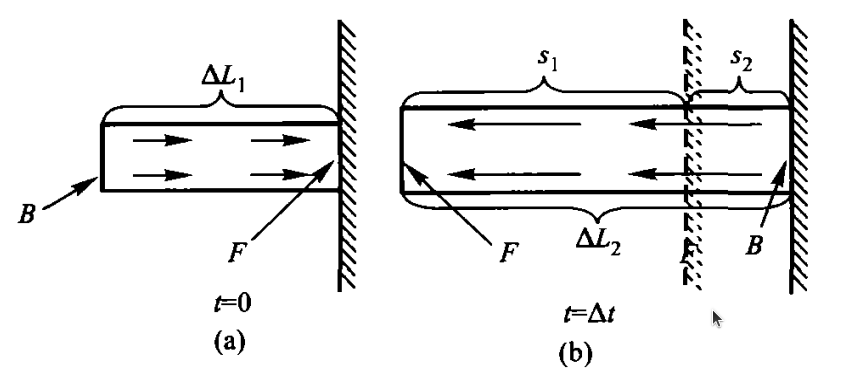
As shown in Figure 2(a), at \(t = 0\), a segment of length \(\Delta L_1\) (\(\Delta L_1 \to 0\)), a monochromatic plane wave with frequency \(\omega_1\) reaches the flat mirror at point \(F\) perfectly. At this moment, the velocity of the flat mirror is \(v\). After a time interval \(\Delta t\), as shown in Figure 2(b), the furthest point \(B\) of this segment of the incident wave reaches the flat mirror. The length of the reflected wave is:

\[\Delta L_2 = s_1 + s_2 \tag{2}\]

Here, \(s_1\) and \(s_2\) are the translation of \(F\) and the mirror during \(\Delta t\) respectively. Since this is an infinitesimally small process, we have:

\[s_1 = c \Delta t \tag{3}\] \[s_2 = v \Delta t \tag{4}\]

Here, \(v\) is the velocity relative to the sun. Also:

\[\Delta t = \frac{\Delta L_1}{c - v} \tag{5}\]

Thus:

\[\Delta L_2 = \frac{c + v}{c - v} \Delta L_1 \tag{6}\]

Because the phase difference between \(F\) and \(B\) is unchanged during reflection, in other words, the number of oscillations contained in the incident wave and the reflected wave remains constant. Therefore, in vacuum:

\[\omega_2 = \frac{c - v}{c + v} \omega_1 \tag{7}\]

Substituting Equation (1), we obtain the energy spectral distribution of the reflected wave:

\[E_2(\omega) = \frac{\omega^3}{\exp\left(\frac{\hbar\omega}{k T_2}\right) - 1} \tag{8}\]

Here:

\[T_2 = \frac{c - v}{c + v} T_1 \tag{9}\]

Thus, the reflected wave corresponds to blackbody radiation at a temperature \(T_2\).

Considering that this process is reversible, assuming the solar sail can be approximated as a heat engine, the efficiency of this process can be determined as:

\[\eta = \frac{T_1 - T_2}{T_1} = \frac{2v}{c + v} \tag{10}\]

In fact, the reflective mirror here can indeed be regarded as a heat engine to which the Carnot theorem can be applied. In the proof of the Carnot theorem, only two characteristics of heat engines are used:

1. Heat is absorbed from a high-temperature heat source and released to a low-temperature heat source.
2. Work is performed.

Evidently, the reflective mirror in this problem satisfies these two requirements and can be considered a heat engine; thus, the Carnot theorem is applicable. Here, light is the heat source rather than part of the heat engine. The flat mirror itself constitutes the heat engine, and since it does not exchange matter with the external world, it is not an open system. Additionally, due to the symmetry of its motion along the direction of propagation, the flat mirror remains in the same state at every position during the process. This is equivalent to the same state of a heat engine (the difference lies only in the temperature of the heat source). Hence, the solar sail can be regarded as a cyclic heat engine with infinitely small steps.

Let’s verify the above derivations from another perspective. From the Work-Energy Theorem, we have:

\[\frac{\frac{E}{c} + \frac{E - \Delta E_k}{c}}{\Delta t} s_2 = \Delta E_k \tag{11}\]

Here, \(E\) is the energy of the incident light, \(\Delta E_k\) is the kinetic energy gained by the flat mirror, and \(c\) is the speed of light. It is easy to get:

\[\eta = \frac{\Delta E_k}{E} = \frac{2v}{c + v} \tag{12}\]

This result agrees with that obtained using the Carnot theorem.

The entorpy of the blackbody radiation is \(4E/3T\). From Equations (6) and (12), it is straightforward to verify that the change of entropy between the incident and reflected radiation is zero, confirming that the above process is indeed reversible.

Finally, it is important to note that one might attempt to address this problem by considering light as a group of photons and using the fact that, after reflection, the energy and momentum of the photon group remain conserved. However, this approach violates the uncertainty principle. Calculations using this method lead to results inconsistent with Equation (7); agreement is only approached when the Planck constant tends toward zero.

---

References

1. Gold T. The Solar Sail and the Mirror. arXiv:physics/0306050v1, 2003.
2. Yam P. Light Sails to Orbit. Scientific American, 2003, 289(5):23.
3. Diedrich B. Letters to the Editors of New Scientist Re: Solar Sailing Breaks Laws of Physics. Online.
4. Zhao Kaihua, Luo Weiyin. New Concepts in Physics: Thermodynamics. Higher Education Press, 1998, p.180.